We need to talk about how we talk about swing - Part 2: Curvature
Finding a better way to quantify swing
Three Ashes Tests down, two to go. Australia 2-1 England. Bazball 3-0 My Nerves. Whoever ends up winning, this is turning into one of the most ridiculous series there has ever been. But for now, let’s put away the short ball, stop passing the No. 3 batting role around, and have a look at some more cricket aerodynamics. That should lower the blood pressure.
This week I’ve decided to return to one of my favourite topics, measuring swing. If you haven’t read Part 1 on the fallacy of quantifying swing with degrees, or would simply like to recap some cricket-related geometry (who wouldn’t?!? - SG), I recommend clicking the link before continuing. It’s a short read, but provides context for this discussion.

I really enjoy it when wickets are taken by swinging deliveries for three reasons:
It’s cool. Swing bowling is cool. People should do more of it.
The TV show lots of slow-mo replays where we can look at the seam position and condition of the ball.
People have to talk about how much swing there is.
The tweet above fits into the 3rd category, and provides me with a starting point to talk about measuring swing, and you guessed it, my first comment is that I don’t like degrees of swing. This is because it depends heavily on the length of the delivery being bowled: Did the ball to dismiss Crawley actually swing more than the rest, or was it just a lot fuller? We don’t have the context to understand what is going on from this measurement alone.
The aim of this post is to introduce a better way to quantify swing, and to recalibrate the discussion away from degrees of swing, and towards what actually matters, curvature. There will be a bit of science, a chunk of maths, followed by some Ashes based examples to round things off. I promise if you get to the end, you will sound a lot cooler when you’re next chatting cricket to your friends. Or at least more likely to use the word ‘parabola’, which is basically the same thing.
Resolving the forces on the ball
Thankfully, understanding why a cricket ball moves in the air doesn’t require a huge amount of mathematical background, and I’ll outline how I approach the problem. First, lets consider the forces acting on the ball. Once the bowler has let go of the ball, the air is the only thing that can impact its motion, other than gravity. As we aren’t particularly interested in how the ball falls through the air, we can ignore gravity along with any aero forces in the vertical direction (these come from the backspin on the ball, but that is for another article).
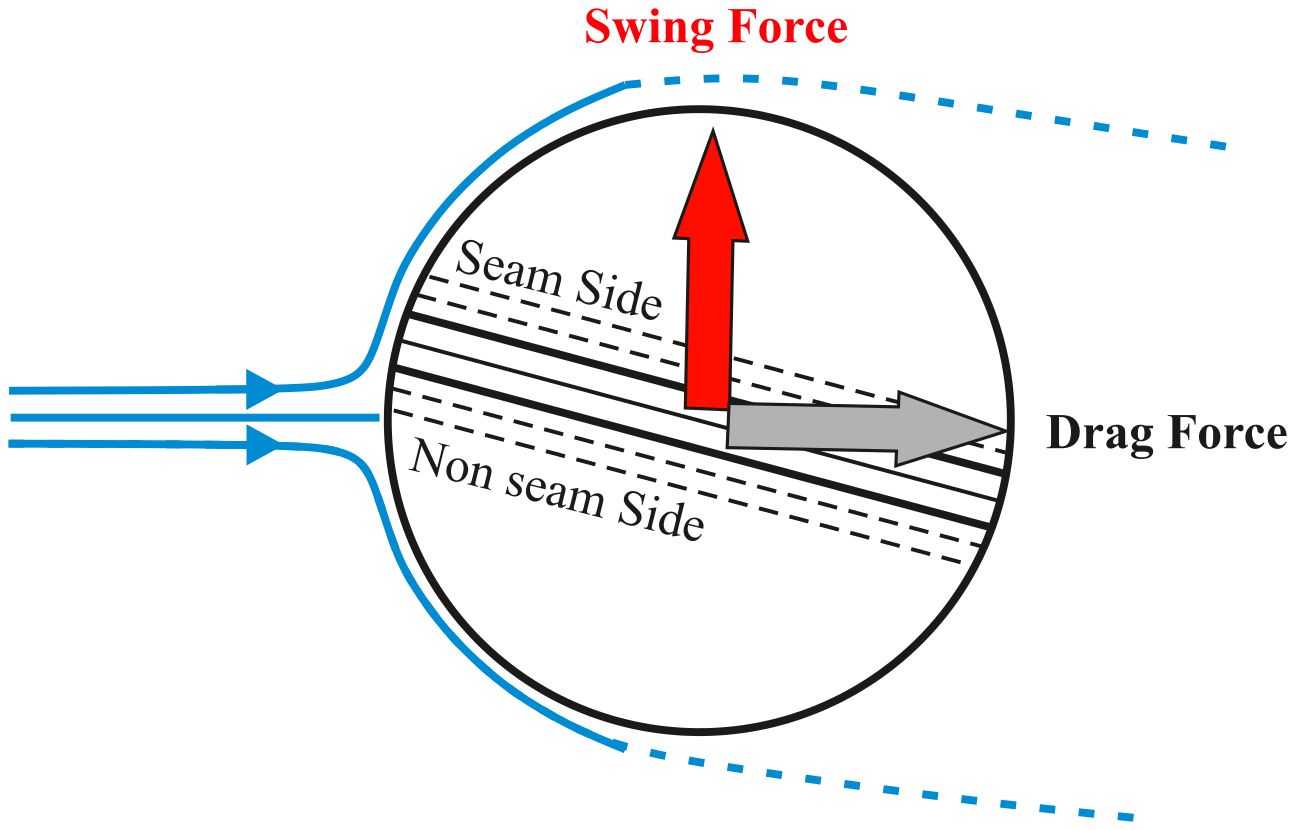
When we think about swing, we are interested in the horizontal swing force on the ball, which makes it move sideways. The other force due to the air is the drag force, which acts in the opposite direction to the motion of the ball, slowing it down. You can see on the diagram above that these forces act at right-angles to one another, which are known as perpendicular forces in technical language.
The nice thing about perpendicular forces is that they can be treated separately when analysing the motion of the ball through the air. When a ball is released, travelling at 85mph for example, the drag force acts to reduce that speed until it bounces. The swing force pushes the ball sideways, increasing its speed in that direction, and making it swing. I won’t go through every assumption that makes this analysis possible, but it holds pretty well for cricket ball trajectories.
The next step is to look at how these two forces make the ball move, and how they affect the shape of the trajectory. Part 1 has an image of a famous Mitchell Starc delivery curving through the air, and it’s this shape which makes swing so dangerous.
What is a parabola?
I’ve mentioned this term a few times already, so I should tell you what it actually means. I hope the maths in this section is fairly easy to follow, even if it harks back to your school days. For now, let’s start with the simple assumption that the swing force acting on the ball is constant throughout its flight. This is not exactly true, but it is a pretty good assumption and simplifies the analysis here. Now, time to dust off the old GCSE textbook and reintroduce our old friends, the SUVAT equations:
For algebraphobes, this equation says: the swing distance, s, is equal to half the sideways acceleration of the ball, a, multiplied by the time it is in the air, t, squared. This is true because when the ball leaves the bowler’s hand, it has no sideways velocity by definition - swing is a change in direction from the initial flightpath. Next, we need to use another classic equation, Newton’s Second Law, which relates the ball’s acceleration, its mass, m, and the force acting on the ball, F:
Here, we have substituted the swing force into the previous equation, using Newton’s Second Law. Now, let’s consider the time taken for the ball to travel down the pitch. For any delivery, the flight time, t, is calculated by dividing the distance between the release point and the bounce point, l, by the average speed of the ball, v. Fuller deliveries spend more time in the air, so this intuitively makes sense. We can now rewrite swing distance in terms of the length of the delivery by substituting out t.
The final piece of the jigsaw requires a small leap of faith, as I don’t want to go into the full maths of calculating the swing force (Hopefully by now you trust that I’ve studied this in enough detail, otherwise I might as well give up!) Put simply this extra information is that the swing force is proportional to the speed of the ball squared. Substituting this last piece into our equation gives us our final approximation for the swing distance:
The decimal number at the front of this equation comes from evaluating some constants, which include the ball size and mass, and the air density. The value in the middle, Cs, is the ‘Swing Coefficient’, which I will come to in a minute. The main thing to take away from this equation is that the swing distance is proportional to the delivery length squared.
This is what I mean by a parabola - a trajectory where the swing increases exponentially as the ball travels through the air. This is why you see the curved shape and this is why the ball appears to swing late, because you gain a large amount more swing by having a fuller delivery length.

So, how does this help us quantify swing better? Well, we now know what type of curve we are dealing with, and so we can define its curvature. For a parabola, the curvature is defined as the ratio of swing distance to the delivery length squared. From the equation above, you can see this is equal to 0.0077Cs. As the decimal number doesn’t change, the Swing Coefficient defines the Curvature of the trajectory and in the rest of this article I use these terms interchangeably. If you ignore the entirety of the rest of this section (which is fair enough), please just remember that.
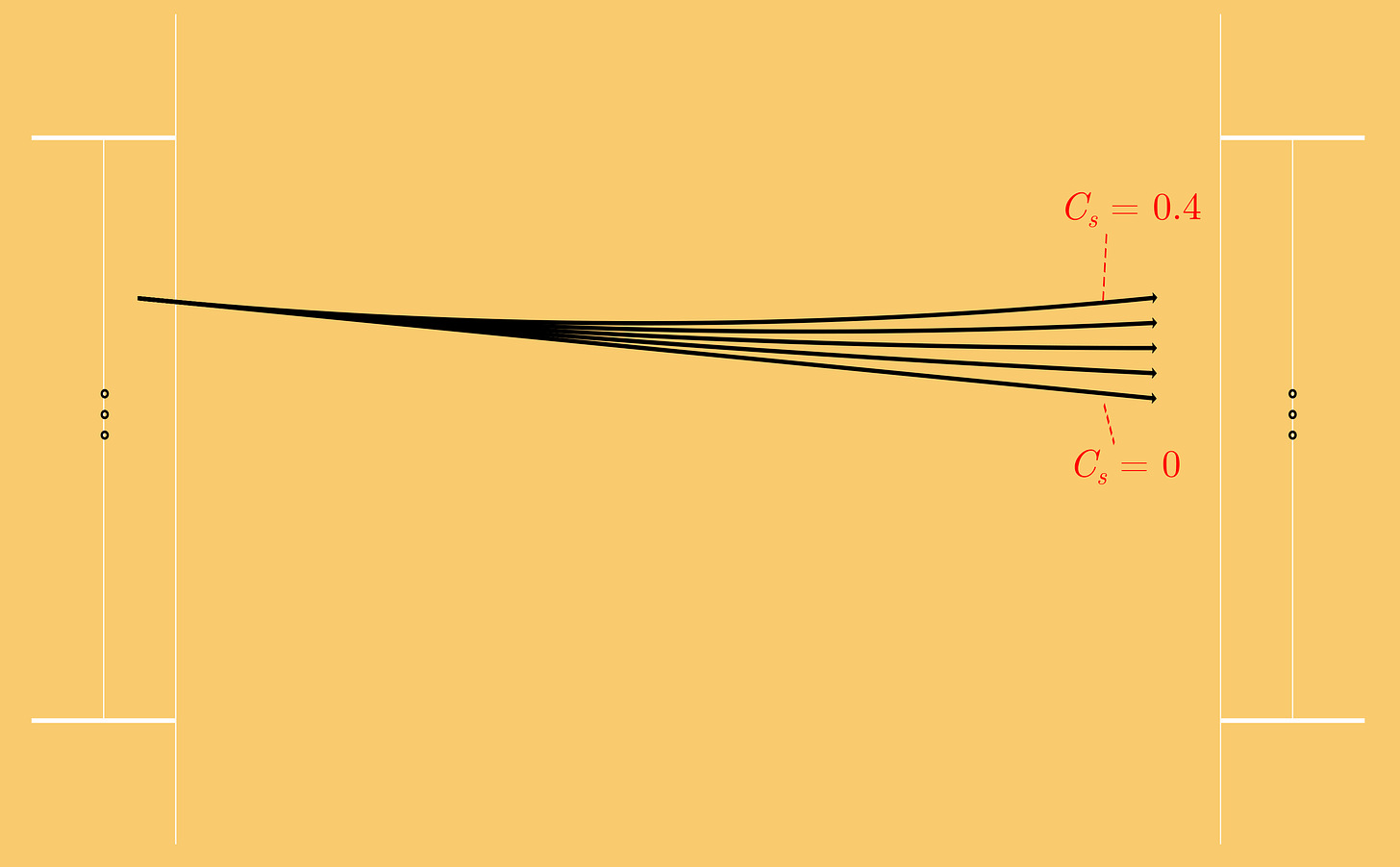
Curvature quantifies how much force acts on the ball
So why have we gone to all of this trouble to define swing in terms of curvature? Well the science tells us that curvature is independent of delivery length, and the swing distance for a given curvature doesn’t depend on the delivery speed. You can see this result from the last equation: the swing distance, s, is not a function of the ball velocity, v. Essentially, knowing the curvature tells us all we need to know about how the ball will swing.
Let’s go back to the example from the start of the article, Marsh to Crawley just after a ball change in England’s second innings. For each delivery, as the length changes, so will the degree of swing that a bowler creates. When the ball is changed, we need to wait for a bowler to bowl a delivery with the same length in order to compare the degrees of swing. With curvature, we can compare deliveries of all lengths. This allows us to see quickly if the swing force being generated is changing, regardless of where the ball is landing.
The ball that dismissed Zak Crawley, which swung 2.7 degrees, was the 6th ball bowled by Mitchell Marsh after the ball was changed. It was also the second fullest - not surprisingly the one that moved 2.9 degrees was the fullest ball bowled in this spell. Crawley also hit two 4s from Marsh before being dismissed, which handily gives us some highlights to compare.

I’ve clipped up the two boundary balls and the wicket side-by-side for comparison. First there is a “length ball”, second a “full ball”, and third the wicket ball, which is the fullest of the three. All of these deliveries swing with the same curvature, more specifically with a Swing Coefficient of about 0.27. This is unsurprising as all three deliveries are bowled at about 80mph with the same age ball and they have a similar seam angle (Marsh bowls a good out-swinger to a right-hander). The physics of each delivery is almost identical.
The only difference was the length of the wicket ball, and the fact that Crawley didn’t smash it for 4. The statistic at the start of the article makes it seem like it was a surprise that the wicket ball swung the most, when, in fact, it was the most likely outcome when you consider the science involved.

The final thing I want to note is that the change in ball really did make it swing more! The curvature of Marsh’s away swinger after the ball change almost doubles, which shows how important ball condition can be for swing, and explains why teams look to change the ball if it stops swinging. This was one of the “things to look for” in my Ashes preview piece, so chalk that up as 1/3 so far (I’m hoping Australia pick Michael Neser for Old Trafford).
Perhaps this measure of swing, whether we call it Swing Coefficient or Curvature, isn’t super intuitive, but hopefully you can agree that it is better than degrees of swing. The average degrees of swing for a spell of bowling is also a tricky metric, as it doesn’t tell you if there are more deliveries that swing or if the deliveries are swinging more. The Swing Coefficient shows you the difference between these two, as you don’t get the variance introduced by the length of each delivery. I’ll discuss this in some more detail another time, as this article is long enough already.
I hope this piece wasn’t too maths heavy and you stuck with it. I’ll be discussing Swing Coefficient a lot more in the future, so this is the reference article if you need it. For now, enjoy the lull between the men’s Ashes Tests, get behind the women’s team, and prepare to look out for some parabolic swing in the upcoming games. Feel free to drop any questions or comments below, and thanks for reading!




Nice article! Quick question...
On Marsh, you say his deliveries mentioned all swung with the same curvature which is predictable due to the fact the ball condition was the same, seam was the same and speed was the same, but earlier you say that that the swing distance for a given curvature doesn’t depend on delivery speed. Confused!